A Digression on ACS and Rules

As you know, ACS offers a simple-yet-powerful rule engine which you can use for processing incoming claims and keep out of your application a considerable chunk of logic: claims set normalization, occasional policy decision point, and so on. The primitive there is the claim mapping rule: if an incoming claim matches the premise of a rule then the conclusion (in form of output claim) is added to the token that ACS will issue. Classic modus ponens, for the first-order logic aficionados among you. In inference rule notation:

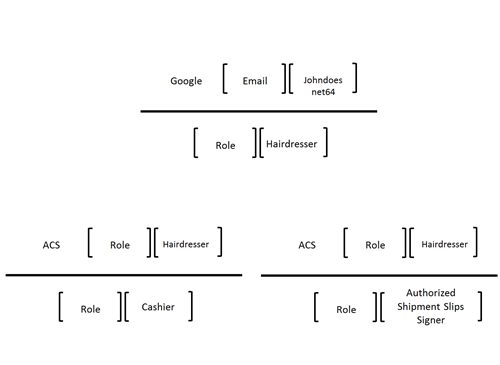
Simply put, that means that I can codify logic such as “if you see a claim coming from Google, of type ‘email’ and with value ‘johndoenet64@gmail.com’ please add to the output token a claim of type ‘role’ and value ‘hairdresser’”. There are variations, for example I can omit claim type and/or value if I want my rule to be triggered for a wider range of inputs (i.e. I might want a rule which gets triggered every time I get something from Google, regardless of which claims are provided: the system rule adding identity provider info is a good example of that), but that’s pretty much it.

One interesting fact you may not be aware of is that ACS rules can be chained: that is, you can create rules which will be triggered by the output of other rules. All you need to do is create a rule whose input claim has ACS itself as issuer.

For example: you could create a rule which assigns to all the users in the role “hairdresser” to the role “cashier” and “authorized shipment slips signer”, two roles associated to the hairdresser position.

The advantages of the chained approach to the “enumeration” one is obvious. If both John and Pamela are hairdressers, with the chaining I need just 4 rules (two for assigning the hairdresser role to the users, two for adding the extra roles to the hairdresser role (which starts looking more like a group)) versus the 6 I’d need without chaining (three rules with email premise and role conclusion per user). That’s N+2 vs 3N… they diverge pretty quickly
Apart from the sheer number of rules, there’s also the manageability of the system. Onboarding Pamela as hairdresser, or changing her position later on, entails just adding (or changing) one single rule. If the hairdresser responsibilities change over time, all you need to do is changing the rules that have role-hairdresser as premise. Neat-o.

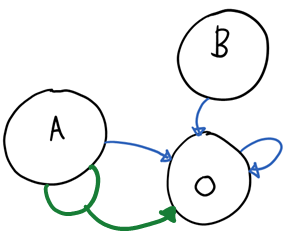
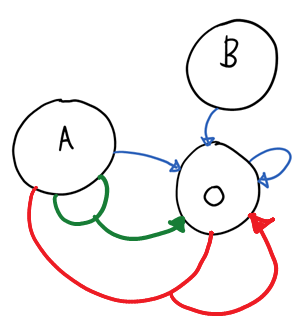
The above is a schema of how the usual rules work. A is the set of all possible claim types/values from the A issuer, O is the set of the claims issued by ACS (B is there just for showing that there can be multiple IPs). The blue arrow from A to O represent rules of the first type, the blue arrow that loops from O to O represents the chained rules. Let’s abuse this notation a bit and give a representation of the two rule styles above.

In the version without chaining, we have 6 rules (all of the form {A,O} predicate) which assign to John and Pamela to the 3 roles.

In the version with chaining, we have two rules of the form {A,O} and two of the form {O,O}. Welcome to the exciting world of predicates.
See what we have done here? The blue rule assigned Joe and Pamela to the set of the hairdressers; the red and green rules got chained and indirectly assigned Joe and Pamela to the set of the signers and the set of the cashiers, too.

The case above is a fairly unfortunate case, as the defining property we are using for determining that a user belongs to a given set (hairdressers) is unique to every element (every user has a different email address) hence in order to define our first set we need to add as many rule as there are users.
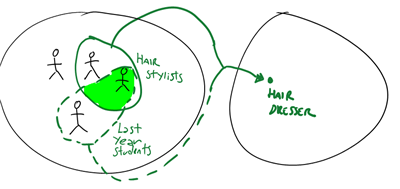
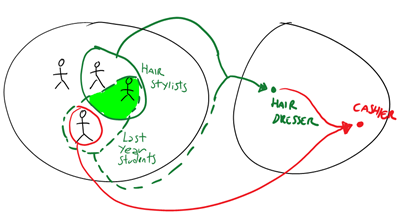
If our users would come from an identity provider that supplies more structured info, such as the directory for a cosmetology school, we could be in a better shape. For example students may be subdivided in groups according to the specialties they elected: hair stylist, skin care, nail technology and so on. Why did I pick up this sample again? Now I have to play along, tho
Anyway, let’s say that those students all go to work in a salon during the summer break, and that salon uses an application secured via ACS. At this point the rule could be “if you see a claim coming from the cosmetology school AD, of type ‘group’ and with value ‘hair stylist’ please add to the output token a claim of type ‘role’ and value ‘hairdresser’”. That rule would instantly cover all the students satisfying the criteria, as opposed to just one as before. You can even extend those sets by boolean union, for example adding a rule which establishes that the Barbering students are also in the Hairdresser role.
The chaining technique would have the same value, refining the properties of one set instead of having to recreate it; but never really doing anything for altering the number of elements affected.

Now what if, instead of the union of sets, we’d want to target the intersection? This is a very, very common requirement. For example, let’s say that the salon will employ only hair stylist students who are at the last year of the course. With the current {A, O} and {O, O} set of predicates, the answer is simple: you can’t. Or better, you can if you “cheat”. You can go by enumeration: if you know in advance that Rudy is a last year student in the hair stylist track, you can provision him by email and do the same with everybody else. That is not always possible, of course, and it’s not very efficient or manageable.
The other possibility is to rely on the directory administration of the school, and ask him/her to create a group “employed at salon A” that can can be used by ACS for assigning the hairdresser role to the correct group. There will be occasions in which you’ll be able to do it, but most often than not you should take as little dependency from the incoming source as possible (no guarantees they are willing to help, or will reliably and timely do so).

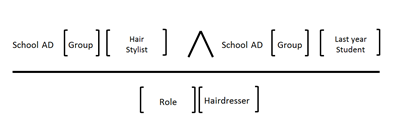
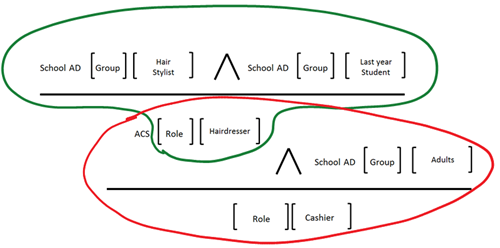
As mentioned here, from today ACS offers a new type of rule which allows you to identify the intersection of two sets. By allowing you to define two input claim conditions in logical AND from the same IP, that is to say a predicate of the form {A&A,O} you can effectively express that
“if you see a claim coming from the cosmetology school AD, of type ‘group’ and with value ‘hair stylist’ AND
you see a claim coming from the cosmetology school AD, of type ‘group’ and with value ‘last year student’
please add to the output token a claim of type ‘role’ and value ‘hairdresser’”.

In other “words”, our diagram earns an extra predicate with different arity:

..and adding a bit of notation abuse, we can see how this new predicate effectively gives you the power of identifying intersections:

Now, you may raise the fact that some conditions may require intersection with more than two sets. That’s fair. The good news is that you can add extra conditions, by feeding the result of one rule as one of the two inputs of another. In other words, you can write rules of the form {A&O, O} (of course the order of A and O in the premise does not matter, as AND is commutative). So if you want one of the students you employ to be allowed to operate a cashier machine only if older than 21, you can cascade the former cashier rule by modifying it as follows:

basically that means we added a predicate of the form shown in red:

Here you can see one case in which no student is actually allowed to operate the cashier:

There is one guy in the “adults” group, but that group has empty intersection with the hairdresser role (which was itself the intersection of the hair stylists and the last year students groups). You can iterate as many times you want, and you can even do intersections entirely in the O domain (with predicates of the form {O&O, O}).

Well, it’s the 3rd blog post I write this weekend, and it’s technically Monday morning now the time is up, I better get some sleep.
The hair salon scenario is perhaps not the most common SaaS application you’ll find around, but I hope this was useful for you to think about how to use ACS rules. If you have feedback on how ACS rules, don’t be shy!