Visual Notation for representing message security

Have you ever found yourself trying to explain to somebody why you need to have a certain certificate installed on a certain machine? Or which token is used to encrypt a certain part of a message? Or maybe when you have to acquire a token, or how you propagate a session key in full security?

Well, I found myself in similar situations many times. I soon discovered that a picture is indeed thousands times better than “you see, you require a token for a certain service so the STS will generate a session key and will encrypt it for that service in the token, while it will produce a requestedprooftoken encrypted with the requestor public key. The requestor will open the requestedproof and call the service, securing the call with the session key and adding the token containing the session key encrypted with the public key of the service and signed with the private key of the STS: the service will the retrieve the session key by decrypting…” and so on and so forth. It’s even better to draw the picture in front of the person, so that you give him/her the time to get the hang of the structure rather than being overwhelmed by the sudden crowd of symbols. If it’s impossible to draw at run time, a good guided walkthrough is still better than the verbal-only alternative.

In the following I describe the notation that I eventually developed for the above described purpose. I’d be happy to hear about alternatives or suggestions, of course. Couple of notes:

• this notation is something I DO, it is NOT official guidance
  
• the purpose of the notation is making people get your point about how you want to secure messages. It is all about clarity, so redundancy is allowed. It is NOT a formal notation, it doesn’t have algebraic closure, etc etc
  
• the notation is not complete, and it may deliberately represent things which are not perfectly corresponding to the truth. For example, you could not draw the addressing headers but still assume they are there; or you could show nested encryption and signature, while maybe the two operatios are applied independently and/or on different parts of the envelope; and so on.

Let’s start with the keys.

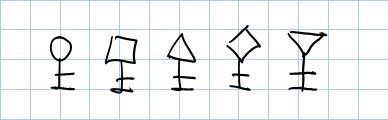	This is how I represent keys. When I want different keys in a single picture, I differentiate them by changing the shape of the keyring: circles, squares, triangles, diamonds… any shape will do.
	Those are X509 certificates. The left part is the public key, the right one the private key. Note that the color is redundant, but it allows you to understand the impications at a glance.
	Public keys. If they are surrounded by the document sign, they are certificates without private keys.
	Private keys.
	Alternate form of private keys, where also the keyring has been halven. very useful when you don’t have colors available, it reinforces the orientation of the picture.
	Symmetric keys. Can be colored or not.

 

Let’s then see how I represent the standard operations.

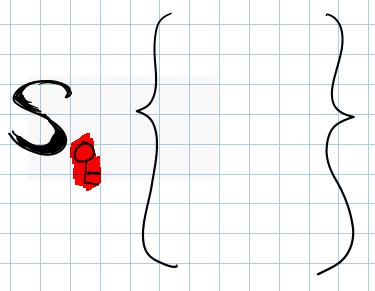	This is a WS-Security signature. Anything inside the brackets will be signed
	Square brackets means that the signature is just a standard XML Signature and it is referring to an XML element, rather than an element of a SOAP ennvelope
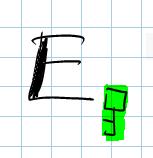	The “E” stands for “Encryption”. Note the use of a public key
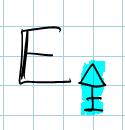	Other keys can be used, of course. Here you can seean encryption operation based on a symmetric key

 

And let’s close with the structures:

 

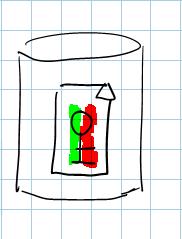	This represents a certificate store.
	This is a token cache, dashed in order to give the feeling of its transient nature. Note the token: similar to a certificate, but with a blue fill pattern

 

Finally, let’s see a couple of examples.

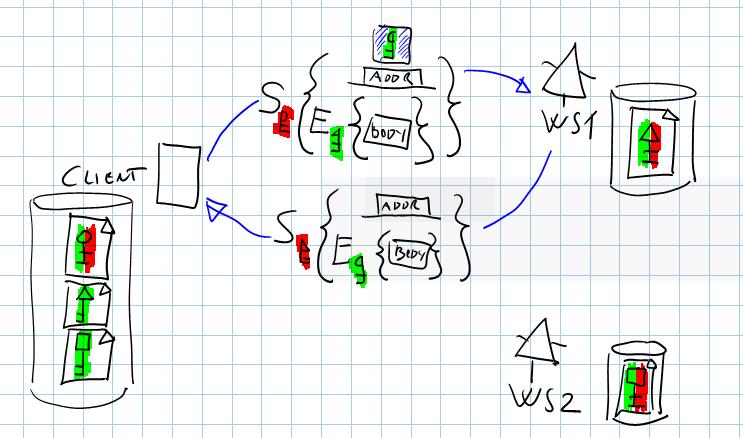
The most WS-Security classic: X509s. Here you can clearly see that a client needs to own the public keys of every service it wants to deal with; furthermore, it is clear that the service can use the client’s public key found in the message and it doesn’t need to keep in the local store the public keys of all possible clients.  Obvious? Maybe to you, my loyal reader, but I can assure you that after showing it  I’ve seen quite a few “aha” moments in the eye of people not familiar with WSS :-).

 

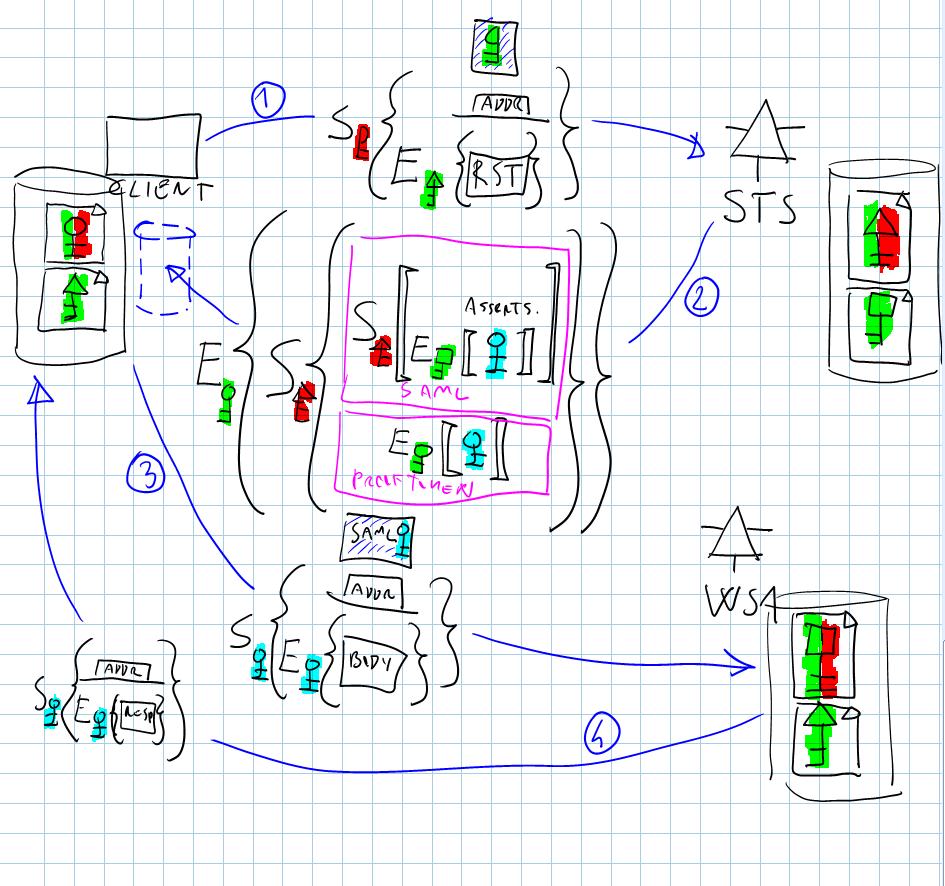
This one is harder. Come with me:

1. the client submits a RequestSecurityToken to the Security Token Service, securing it in the classic way, intended to be used with WS1
   
2. the STS answer a SAML token (which is signed by the authority and contains a symmetric key, in turquoise, encrypted with the public key of WS1) and a proof token, containing the session key encrypted with the client’s public key
   
3. the client extract the session key from its prooftoken, the uses such a key to secure a call to WS1. It adds to the call the SAML received in 2)
   
4. WS1 decrypt the key inside the SAML and use it to consume the message

This walkthrough makes many thing evident, including the fact that the client don’t need anymore to keep WS public keys (with the notable exception of the STS); it also suggests that everytime you want to talk to a different service you need to have a new SAML reissued to you in order to havew the session key encrypted for the right target.